第10回 アヤメの分類
今回のテーマはアヤメの分類です。分類には決定木とランダムフォレストを用います。決定木には分類木と回帰木がありますが、今回使うのは分類木です。ランダムフォレストは決定木にアンサンブル学習を組み合わせた手法です。解説動画では決定木とランダムフォレストについて解説しているので、まずはそちらをご覧ください。
今回の実装のソースコードはこちらからダウンロードできます。
目次
解説動画
Part1
Part2
概要
実装内容
代表的な機械学習フレームワークである scikit-learn を用いて、アヤメのデータセット(Iris plants dataset)から決定木とランダムフォレストによる分類を行います。
実装環境
Google Colaboratoryを使用します。Google Colaboratoryに関する説明はこちらをご覧ください。
データセットについて
アヤメのデータセットは、3種類のアヤメの品種ごとに、がく片や花弁のサイズを測定したデータセットです。 このデータセットを用いて、がく片や花弁のサイズから品種を予測することを試みます。
ちなみに、アヤメのデータセットの作者は、推測統計学を確立したことで有名な R.A. Fisher です。
アヤメのデータセットの概要:
- 総サンプル数は150件
- 3つの品種ごとに50件ずつのデータ
- 特徴量(説明変数)
- sepal length (cm): がく片の長さ(cm単位)
- sepal width (cm): がく片の幅(cm単位)
- petal length (cm): 花弁の長さ(cm単位)
- petal width (cm): 花弁の幅(cm単位)
- 正解ラベル(目的変数)※アヤメの品種
- 0: setosa
- 1: versicolor
- 2: virginica
イメージとしては次の画像のとおり(画像出典: https://rpubs.com/Jay2548/519589 )。



画像を見ると何となくSepal(がく片)よりPetal(花弁)の方が品種によって差がありそうです。
実装
データセット
データセットの読み込み
scikit-learn に組み込まれているデータセットから、アヤメのデータセットを読み込んで利用します。
データセットの読み込みには sklearn.datasets.load_iris を用います。
from sklearn.datasets import load_iris
iris = load_iris()Pythonの組込み関数 dir を用いると、引数で指定したオブジェクトの属性のリストを取得できます。
print(dir(iris))['DESCR', 'data', 'data_module', 'feature_names', 'filename', 'frame', 'target', 'target_names']
それぞれ次のとおり。
| 属性 | 内容 |
|---|---|
| DESCR | データセットに関する説明 |
| data | サンプルごとの特徴量(説明変数) |
| feature_names | 特徴量の名称 |
| filename | ファイル名 |
| target | 正解ラベル(目的変数) |
| target_names | 正解ラベルの名称 |
特徴量の名称を表示
print(iris.feature_names)['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
正解ラベルの名称を表示
print(iris.target_names)['setosa' 'versicolor' 'virginica']
先頭から5サンプル分の特徴量を表示
print(iris.data[:5])[[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2]]
全サンプルの正解ラベルを表示
print(iris.target)[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
ラベルの偏りはなさそうです。
データセットの可視化
グラフ描画用にデータフレームを作成します。
import pandas as pd
# 特徴量のデータフレームを作成
df_feature = pd.DataFrame(iris.data, columns=iris.feature_names)
# 正解ラベルのデータフレームを作成
df_target = pd.DataFrame(iris.target, columns=['species'])
# 正解ラベルが数値なので、分かりやすいように名称に変換
df_target.replace({0: 'setosa', 1: 'versicolor', 2:'virginica' }, inplace=True)
# 特徴量のデータフレームと正解ラベルのデータフレームを連結
# axis=1 と指定することで、列方向に連結する
df_iris = pd.concat([df_feature, df_target], axis=1)pandas.DataFrame.describe で次の記述統計量を計算できます。
- データのサンプル数
- 平均値
- 標準偏差
- 最小値
- 第一四分位数
- 第二四分位数(中央値)
- 第三四分位数
- 最大値
これらの値からデータの大まかな傾向を把握することができます。
df_iris.describe()| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.057333 | 3.758000 | 1.199333 |
| std | 0.828066 | 0.435866 | 1.765298 | 0.762238 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 |
散布図行列をプロットすると、視覚的に分かりやすくなります。
散布図行列は2つの変数の組み合わせに対して散布図を作成し行列にまとめたもので、変数同士の相関関係を視覚的に確認することができます。
散布図行列のプロットにはパッケージ seaborn と matplotlib を使用します。
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
sns.pairplot(df_iris, hue='species', diag_kind='hist')
plt.show()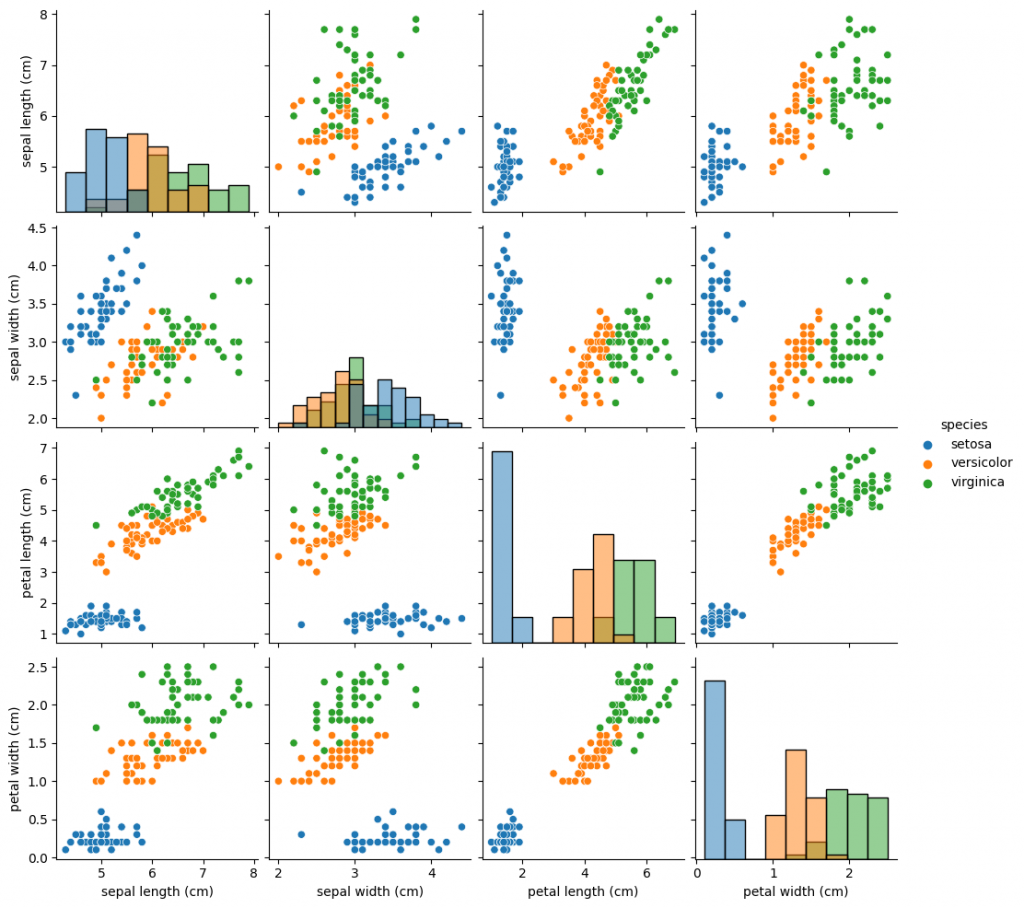
どの特徴量を使用してもsetosaとそれ以外は比較的容易に分類できそうであることが分かります。 また、versicolorとvirginicaは特徴量によって分類しやすそうな場合と分類しにくそうな場合があることが分かります。例えばsepal widthとsepal lengthの組合せはversicolorとvirginicaが混ざり合っていて、分類のための境界を引くのが難しそうです。
データセットの分割
データセットを、学習用 : 評価用 = 7 : 3 の割合で分割します。 データセットの分割には、関数 sklearn.model_selection.train_test_split を用います。
- 第1引数 : 特徴量のデータを指定
- 第2引数 : 正解ラベルのデータを指定
test_size: 評価用データの割合(0.0~1.0)を指定random_state: 乱数シード
データセットの分割時にサンプルの順番をランダムに入れ替えてから分割を行っています。乱数シードを設定しないと実行する度に結果が変わってしまいますが、乱数シードを設定しておけば再現性を担保できます。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=0)決定木による分類
学習
決定木はクラス sklearn.tree.DecisionTreeClassifier で実装されています。
ドキュメント:sklearn.tree.DecisionTreeClassifier
学習の仕方は次のとおり:
sklearn.tree.DecisionTreeClassifierのインスタンスを作成- 引数
criterionに不純度を指定 - 引数
max_depthに木の深さを指定 - 引数
random_stateに乱数シードを指定
- 引数
- インスタンスのメソッド
fitを実行- 第1引数に学習用データの特徴量を指定
- 第2引数に学習用データの正解ラベルを指定
ここでは criterion='gini' 、 max_depth=3 と設定してみます。
※後でランダムフォレストの結果と比較を行いますが、その際は条件を合わせるため、上記の設定を用いることにします。
from sklearn.tree import DecisionTreeClassifier
model_dt = DecisionTreeClassifier(criterion='gini', max_depth=3, random_state=0)
model_dt.fit(X_train, y_train)学習済みの決定木をグラフに描画します。 グラフの描画には Graphviz を使用しますが、Colabratory には最初からインストール済みのため、特別な設定は必要ありません。
import pydotplus
from io import StringIO
from IPython import display
from sklearn.tree import export_graphviz
data = StringIO()
export_graphviz(model_dt,
out_file=data,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True,
rounded=True)
graph = pydotplus.graph_from_dot_data(data.getvalue())
display.display(display.Image(graph.create_png()))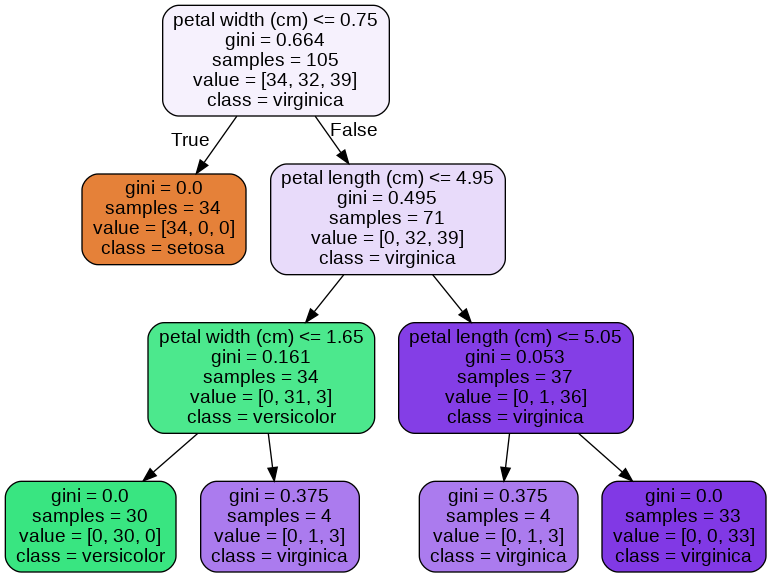
学習済みの決定木から特徴量の重要度を取得できます。
sklearn.tree.DecisionTreeClassifier の属性 feature_importances_ が特徴量の重要度です。
特徴量の重要度を横棒グラフでプロットすると次のようになります。
plt.barh(y=iris.feature_names, width=model_dt.feature_importances_)
plt.grid(True)
plt.xlabel('feature importance')
plt.ylabel('feature')
plt.show()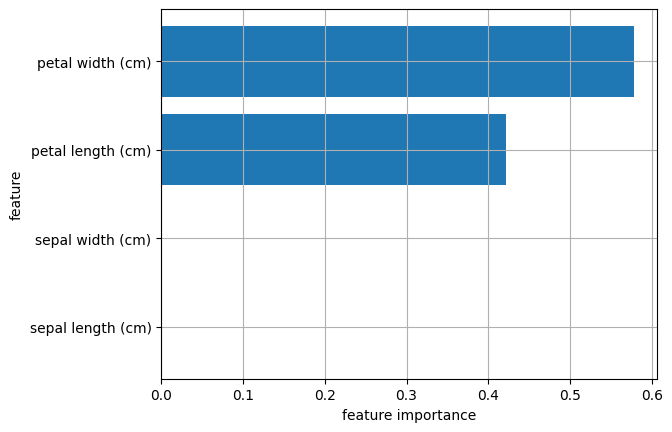
グラフから、4つの特徴量について次のことが分かります:
- petal width と petal length の重要度が大きい
- sepal width と sepal length の重要度は0
つまり、この決定木はがく片の幅と長さ(sepal width、sepal length)ではなく、花弁の幅と長さ(petal width、petal length)のみを分類の指標としているということです。
実際、上で可視化した木構造では、petal width と petal length しか使用されていません。
サンプルの画像や散布図からもある程度想像できますが、決定木を使うことで定量的にどの特徴量が分類にとって重要なのかという事が分かります。
予測
学習済みモデルを用いて、評価用データについて予測を行います。 予測にはメソッド predict を用います。引数に評価用データを指定します。
y_predict = model_dt.predict(X_test)評価
続いて、予測結果の精度を評価します。 様々な評価指標がありますが、ここでは、正解率(accuracy)、混同行列(confusion matrix)、適合率(precision)、再現率(recall)、F1値(F1 score)を計算します。
※各評価指標については「第4回 深層学習による画像分類」の学習-評価の章で説明しています。詳しく知りたい方はそちらをご覧ください。
正解率は関数 sklearn.metrics.accuracy_score を用いて計算できます。
from sklearn.metrics import accuracy_score
acc = accuracy_score(y_test, y_predict)
print(f'{acc:.3f}')0.978
混同行列は関数 sklearn.metrics.confusion_matrix を用いて計算できます。
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_predict)
print(cm)[[16 0 0] [ 0 17 1] [ 0 0 11]]
適合率、再現率、F1値は、関数 sklearn.metrics.classification_report を用いて計算できます。
from sklearn.metrics import classification_report
report = classification_report(y_test, y_predict, target_names=iris.target_names, digits=3)
print(report) precision recall f1-score support
setosa 1.000 1.000 1.000 16
versicolor 1.000 0.944 0.971 18
virginica 0.917 1.000 0.957 11
accuracy 0.978 45
macro_avg 0.972 0.981 0.976 45
weighted_avg 0.980 0.978 0.978 45
これらの評価指標を見ると、setosaは完璧に分類できていますが、versicolorをvirginicaと誤って予測しているデータが1つあることが分かります。
ランダムフォレストによる分類
続いてランダムフォレストでも分類してみます。
ランダムフォレストはクラス sklearn.ensemble.RandomForestClassifier で実装されています。
ドキュメント:sklearn.tree.DecisionTreeClassifier
学習
決定木の場合と同様に、インスタンスを作成して、メソッド fit を実行します。
決定木の結果と比較したいので、条件を揃えます(criterion=’gini’, max_depth=3)。
from sklearn.ensemble import RandomForestClassifier
model_rf = RandomForestClassifier(criterion='gini', max_depth=3, random_state=0)
model_rf.fit(X_train, y_train)特徴量の重要度をプロット
plt.barh(y=iris.feature_names, width=model_rf.feature_importances_)
plt.grid(True)
plt.xlabel('feature importance')
plt.ylabel('feature')
plt.show()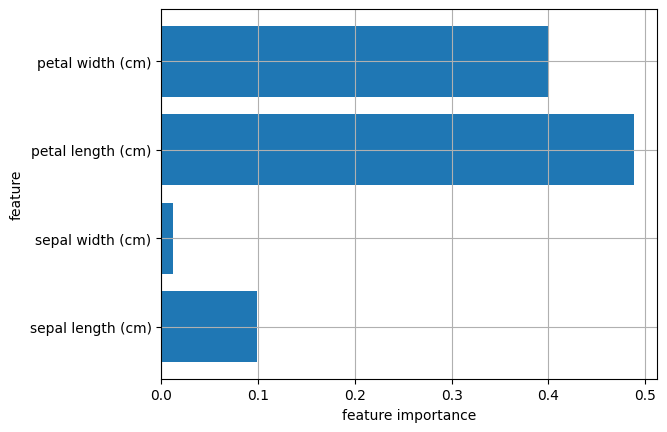
決定木とは違い、sepal widthとsepal lengthの重要度が0ではなくなっています。
予測
y_predict = model_rf.predict(X_test)0.978
評価
acc = accuracy_score(y_test, y_predict)
print(f'{acc:.3f}')[[16 0 0] [ 0 17 1] [ 0 0 11]]
report = classification_report(y_test, y_predict, target_names=iris.target_names, digits=3)
print(report) precision recall f1-score support
setosa 1.000 1.000 1.000 16
versicolor 1.000 0.944 0.971 18
virginica 0.917 1.000 0.957 11
accuracy 0.978 45
macro_avg 0.972 0.981 0.976 45
weighted_avg 0.980 0.978 0.978 45
ランダムフォレストの結果は決定木と同じでした。 これはデータセットが比較的単純なので、単純な決定木でも十分に分類できていたためと考えられます。
まとめ
決定木とランダムフォレストでアヤメの分類をしました。決定木は木をグラフに可視化したり、重要度を計算することで解釈性の高いモデルを構築することが可能です。 また、今回はあまり違いは見られませんでしたが、ランダムフォレストを用いることで、より精度の高い予測が可能になります。そのため、解釈・説明のしやすさを重視するなら決定木、予測精度を重視するならランダムフォレストといった使い分けをするのが良いでしょう。
次回はワインのデータセットを例にクラスタリングの解説を行います。
最後までお読みいただきありがとうございました。それでは引き続きよろしくお願いいたします。




