第11回 ワインのクラスタリング
今回のテーマはワインのクラスタリングです。クラスタリングは機械学習の基礎的なタスクの一つであり、教師なし学習の一種です。クラスタリングの場合、回帰や分類とは異なり、予め正解となる教師データがありません。正解データがなくても、データそのものから規則性を見出して類似したものをグルーピングし、クラスターと呼ばれる集合を作ります。各クラスターの特徴を捉えることでデータの分析に役立てることができます。
今回の実装のソースコードはこちらからダウンロードできます。
目次
解説動画
概要
実装内容
代表的な機械学習フレームワークである scikit-learn を用いて、ワインのデータセットからk-means法によるクラスタリングを行います。
実装環境
Google Colaboratoryを使用します。Google Colaboratoryに関する説明はこちらをご覧ください。
データセットについて
ワインのデータセットは次の特徴量からなる178件のデータです。
| 特徴量 | 内容 |
|---|---|
| alcohol | アルコール度数 |
| malic_acid | リンゴ酸 |
| ash | 灰 |
| alcalinity_of_ash | 灰のアルカリ度 |
| magnesium | マグネシウム |
| total_phenols | 全フェノール |
| flavanoids | フラボノイド |
| nonflavanoid_phenols | 非フラボノイドフェノール |
| proanthocyanins | プロアントシアニジン |
| color_intensity | 色の濃さ |
| hue | 色相 |
| od280/od315_of_diluted_wines | 希釈ワインのOD280/OD315 (波長が280nmと315nmの光の吸光度の比) |
| proline | プロリン |
ワインのデータセットには元々classという目的変数となる品種を表すラベルがついていますが、今回はラベルの情報は利用せずにクラスタリングを行ってみます。また、今回は可視化を容易にするためにalcoholとod280/od315_of_diluted_winesの2つの変数のみを使用することにします。
実装
データセットの読み込み
scikit-learnに組み込まれているデータセットから、ワインのデータセット(Wine dataset)を読み込んで利用します。
データセットの読み込みには sklearn.datasets.load_wine を用います。
from sklearn.datasets import load_wine
wine = load_wine()Pythonの組込み関数 dir を用いると、引数で指定したオブジェクトの属性のリストを取得できます。
dir(wine)['DESCR', 'data', 'feature_names', 'target', 'target_names']
各項目の内容はそれぞれ次のとおりです。
| 属性 | 内容 |
|---|---|
| DESCR | データセットに関する説明 |
| data | データごとの特徴量(説明変数) |
| feature_names | 特徴量の名称 |
| target | 目的変数 |
| target_names | 目的変数の名称 |
特徴量の名称を表示してみます。
wine.feature_names['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
次に pandas を用いて特徴量からデータフレームを作成します。
import pandas as pd
df = pd.DataFrame(wine.data, columns=wine.feature_names)今回は2つの特徴量(alcoholとod280/od315_of_diluted_wines)のみを使用してクラスタリングを行うため、データフレームからalcoholとod280/od315_of_diluted_wines以外の特徴量を削除します。
columns = ['alcohol', 'od280/od315_of_diluted_wines']
df = df[columns]先頭から5データ分の特徴量を表示してみます。
df.head()| alcohol | od280/od315_of_diluted_wines | |
|---|---|---|
| 0 | 14.23 | 3.92 |
| 1 | 13.20 | 3.40 |
| 2 | 13.16 | 3.17 |
| 3 | 14.37 | 3.45 |
| 4 | 13.24 | 2.93 |
pandas.DataFrame.describe で平均値や標準偏差などの記述統計量を計算できます。これらからデータの大まかな傾向を把握することができます。
df.describe()| alcohol | od280/od315_of_diluted_wines | |
|---|---|---|
| count | 178.000000 | 178.000000 |
| mean | 13.000618 | 2.611685 |
| std | 0.811827 | 0.709990 |
| min | 11.030000 | 1.270000 |
| 25% | 12.362500 | 1.937500 |
| 50% | 13.050000 | 2.780000 |
| 75% | 13.677500 | 3.170000 |
| max | 14.830000 | 4.000000 |
matplotlib を用いてグラフにプロットしてみます。
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(7, 5))
plt.scatter(x=df[columns[0]], y=df[columns[1]])
plt.xlabel(columns[0])
plt.ylabel(columns[1])
plt.grid()
plt.show()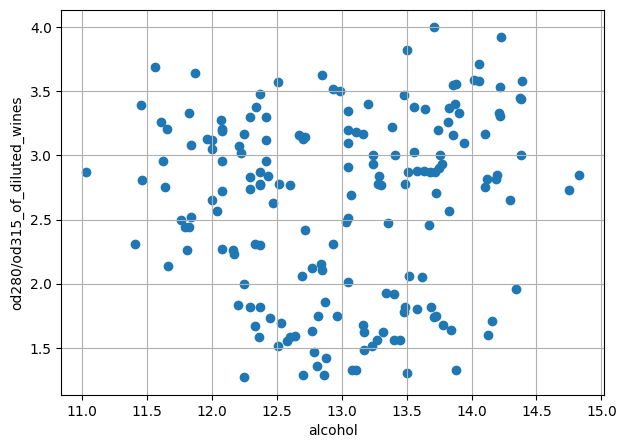
おおよそ3つのクラスターに分けられそうです。
前処理
取得したデータはそのままでは解析に適さない場合があります。 例えば次のようなケースが挙げられます。
- 変数ごとに単位やスケールが異なる
- データが存在しない(欠損値)
- データに異常がある(外れ値)
このようなデータを”きれい”にして、解析に適したデータに変換することを前処理と呼びます。
今回使用するデータは比較的きれいなため、スケールの調整のみを行います。
標準化
平均が0で標準偏差が1となるようにスケールを変換することを標準化といいます。
scikit-learn で標準化を実行するには sklearn.preprocessing.StandardScaler.fit_transform を使用します。
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
df_scaled = pd.DataFrame(ss.fit_transform(df), columns=columns)正しく標準化されているか確認してみます。
df_scaled.describe()| alcohol | od280/od315_of_diluted_wines | |
|---|---|---|
| count | 1.780000e+02 | 1.780000e+02 |
| mean | 7.943708e-15 | 2.235415e-15 |
| std | 1.002821e+00 | 1.002821e+00 |
| min | -2.434235e+00 | -1.895054e+00 |
| 25% | -7.882448e-01 | -9.522483e-01 |
| 50% | 6.099988e-02 | 2.377348e-01 |
| 75% | 8.361286e-01 | 7.885875e-01 |
| max | 2.259772e+00 | 1.960915e+00 |
確かに2つの変数ともmean(平均値)がほぼ0、std(標準偏差)がほぼ1となっていることが分かります。
k-means法によるクラスタリング
sklearn.cluster.KMeans を使用して、上記で標準化したデータセットに対して、k-means法によるクラスタリングを実行してみます。
ここでは以下のパラメータを指定します:
- n_clusters:クラスター数
- init:セントロイド初期化方法(※’random’:k-means法)
- random_state:乱数シード
n_clusters=3、 init=’random’で実行してみます。random_state の値は何でも良いですが、アルゴリズムの中で乱数を使用しているため、randim_state の値を同じ値に固定しておくと何回実行しても同じ結果を再現することが来ます。
なお、クラスタリングの実行に用いられるメソッドとしては以下のものがあります:
- sklearn.cluster.KMeans.fit:クラスタリングの計算を実行する。
- sklearn.cluster.KMeans.predict:各データのクラスターラベルを求める。
- sklearn.cluster.KMeans.fit_predict:クラスタリングの計算を実行し、各データのクラスターラベルを求める。
ここでは sklearn.cluster.KMeans.fit_predictを用いて、クラスタリングの実行とクラスターラベルの取得を同時に行います。
from sklearn.cluster import KMeans
# モデルの生成
model = KMeans(n_clusters=3, init='random', random_state=0)
# クラスタリングを実行
y_pred = model.fit_predict(df_scaled)sklearn.cluster.KMeans.fit_predict の戻り値は各データに対するクラスターのラベルになっています。
y_predarray([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 2, 0, 0, 0,
2, 0, 1, 0, 1, 2, 2, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1], dtype=int32)
クラスターのラベルが {0, 1, 2} の3種類あることが分かります。データセットが3つのクラスターに分割されたようです。
matplotlib と seaborn を用いてクラスターごとに色分けしてグラフにプロットしてみます。
import seaborn as sns
# クラスターラベルと入力データを結合
df_cluster = pd.concat([pd.DataFrame(df_scaled, columns=columns),
pd.DataFrame(y_pred, columns=['cluster'])],
axis=1)
plt.figure(figsize=(7, 5))
# データのプロット
sns.scatterplot(x=columns[0], y=columns[1], data=df_cluster, s=60,
hue='cluster', palette=sns.color_palette('muted', 3))
# セントロイドのプロット
centroids = model.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', color='k', label='centroid')
plt.legend()
plt.grid()
plt.show()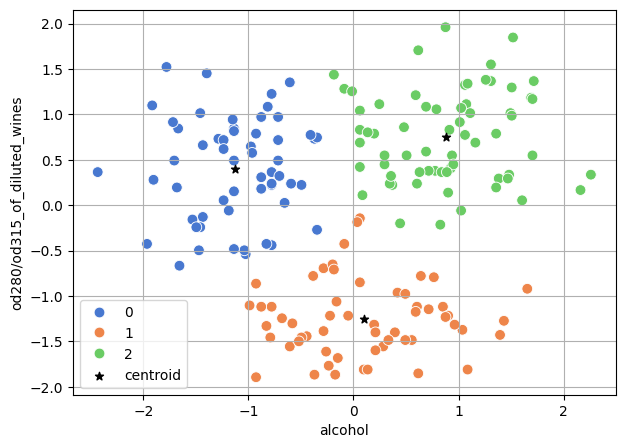
クラスタリングの評価
先ほどのクラスタリングの結果ではクラスター数が3になっていました。ところで、このクラスター数が3であることは妥当なのでしょうか?
ここではクラスター数の妥当性をエルボー法とシルエット分析により評価してみます。
エルボー法
エルボー法の手順は次のとおりです:
- クラスター数を変化させながらクラスタリングを行う
- クラスター数とクラスター内誤差平方和(SSE)の関係をプロットする
- グラフからSSEの減少幅が緩やかになる転換点を見出し、そのクラスター数を最善のものとする
クラスター数を1から10まで変化させてクラスタリングし、SSEをプロットしてみます。
今回はクラスターラベルを求める必要はないので、sklearn.cluster.KMeans.fitを使用します。
また、SSEは sklearn.cluster.KMeans の属性 inertia_ から取得できます。
# クラスタリング実行
cluster_range = range(1, 11)
SSEs = []
for i in cluster_range:
model_tmp = KMeans(n_clusters=i, init='k-means++', random_state=0)
model_tmp.fit(df_scaled)
# SSEの取得
SSEs.append(model_tmp.inertia_)
# グラフにプロット
plt.plot(cluster_range, SSEs, marker='o')
plt.xlabel('number of clusters')
plt.ylabel('SSE')
plt.show()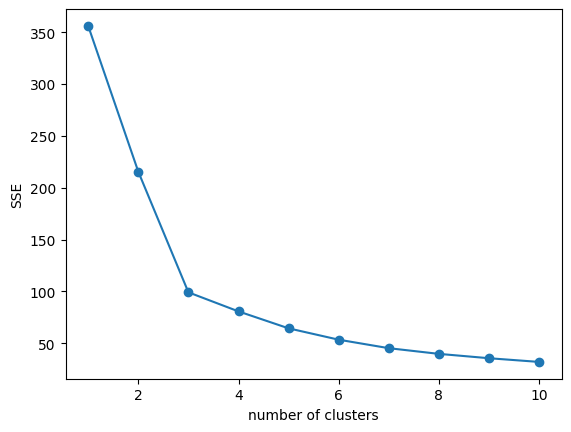
クラスター数3のところが”肘”となっているため、クラスター数3が最適なのだと判断できます。
シルエット分析
シルエット分析では、データごとにシルエット係数を計算し、クラスターごとに大きい順に並べます。
シルエット係数は sklearn.metrics.silhouette_samples で計算できます。また、 sklearn.metrics.silhouette_score でデータ全体のシルエット係数の平均値を計算できます。
scikit-learnのサンプルページを参考にシルエット図をプロットしてみます。
import numpy as np
from sklearn.metrics import silhouette_samples, silhouette_score
# クラスター数
n_clusters = 3
# クラスターラベル
cluster_labels = y_pred
# シルエット係数の平均値を計算
silhouette_avg = silhouette_score(df_scaled, cluster_labels)
# 各データのシルエット係数を計算
sample_silhouette_values = silhouette_samples(df_scaled, cluster_labels)
# シルエット図の描画
y_lower = 10
for i in range(n_clusters):
ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = plt.cm.nipy_spectral(float(i) / n_clusters)
plt.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
plt.text(-0.02, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
# 平均線の描画
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.tick_params(labelleft=False)
plt.xlabel('silhouette')
plt.ylabel('cluster')
plt.show()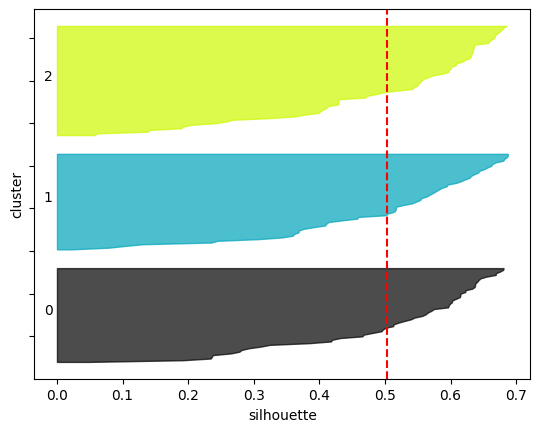
クラスターごとのデータ数や各クラスターのシルエット係数も同じような値になっているため、クラスタリング結果としてはバランスが取れたものとなっていると言えます。
まとめ
k-means法によるクラスタリングを行いました。クラスタリングは教師なし学習の一種で、回帰や分類のような教師あり学習とは異なり、正解データがない状態でもデータの中に潜む規則性を見出すことができます。顧客データの分析などにも応用できます。
これでAIセミナーは完結です。最後までお読みいただきありがとうございました。これまでに身に着けた基礎知識を元に身の回りの課題にぜひ応用してみてください!




