第9回 住宅価格の予測
今回のテーマは住宅価格の予測です。機械学習の基礎的なタスクである「回帰」を用いて分析を行います。
今回の実装のソースコードはこちらからダウンロードできます。
目次
解説動画
概要
- 実装内容
- 代表的な機械学習フレームワークである scilit-learn を用いて、部屋の面積など様々な変数から、その住宅の価格を予測する回帰分析を行います。
- 実装環境
- Google Colaboratoryを使用します。Google Colaboratoryに関する説明はこちらをご覧ください。
実装
データセットの取得
scikit-learn の sklearn.datasets.fetch_openml を使用して、データセット house_prices を読み込みます。 このデータセットは、アイオワ州エイムズの住宅ついて、79個の説明変数と1個の目的変数から構成されています。
from sklearn.datasets import fetch_openml
housing = fetch_openml(name="house_prices", as_frame=True)オリジナルのデータセットは説明変数が多い(79個ある)ため、やや天下り的ではありますが、ここでは予め、目的変数との相関が比較的高い下記の変数に絞った上で使用します。
| 説明変数 | 概要 |
|---|---|
| YearBuilt | 建築年月日 |
| YearRemodAdd | リフォーム年月日(増改築がない場合は建築年月日と同じ) |
| TotalBsmtSF | 地下室の合計面積(平方フィート) |
| 1stFlrSF | 1階面積(平方フィート) |
| GrLivArea | 地上の居住エリアの面積(平方フィート) |
| FullBath | 地上のフルバスルーム |
| TotRmsAbvGrd | 地上の部屋数の合計(バスルームを除く) |
| GarageCars | 車の収容台数に応じたガレージのサイズ |
| GarageArea | ガレージの面積(平方フィート) |
また、目的変数は SalePrice であり、住宅の販売価格を表しています。
import pandas as pd
# データセットのうち、使用するカラム
columns = [
'YearBuilt', 'YearRemodAdd', 'TotalBsmtSF', '1stFlrSF', 'GrLivArea',
'FullBath', 'TotRmsAbvGrd', 'GarageCars', 'GarageArea']
# 説明変数
X = housing.data[columns]
# 目的変数
y = housing.target
# 以降での解析のため、説明変数と目的変数を1つのデータフレームに結合しておく
df = pd.concat([X, y], axis=1)shapeを使うとデータフレームのサイズを取得できます。
df.shape(1460, 10)この結果から、1,460行×10列のデータフレームであることが分かります。
- データフレームの行が各サンプルを表しており、1,460個のサンプルがある。
- データフレームの列が9個の説明変数と1個の目的変数(※上記で説明変数と目的変数を列方向に結合したため)を表している。
説明変数の選択
回帰分析で使用する説明変数を選択するために、目的変数と相関が高いものを選ぶ必要があります。 そこで、説明変数と目的変数の相関を調べるため、散布図行列を作成してみます。 散布図行列の描画には seaborn.pairplot を使用します。
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='whitegrid')
sns.pairplot(df, height=1.5)
plt.show()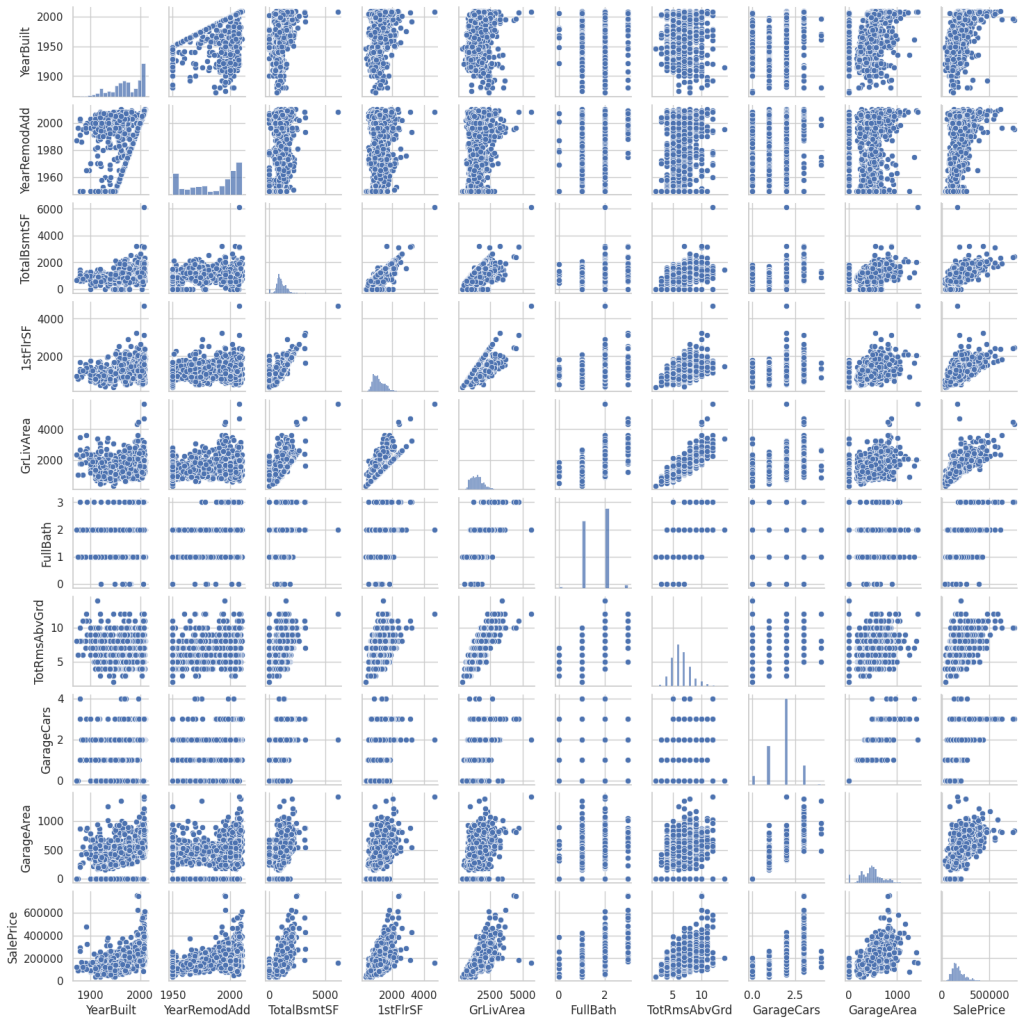
散布図行列は視覚的に変数間の相関を把握できますが、定量的に把握するには相関係数を計算する必要があります。 numpy.corrcoef で相関係数を計算し、seaborn.heatmap でヒートマップとして表示してみます。
import numpy as np
# 相関係数の計算
cm = np.corrcoef(df.values.T)
# ヒートマップとして表示
plt.figure(figsize=(10, 7))
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', xticklabels=df.columns, yticklabels=df.columns)
plt.show()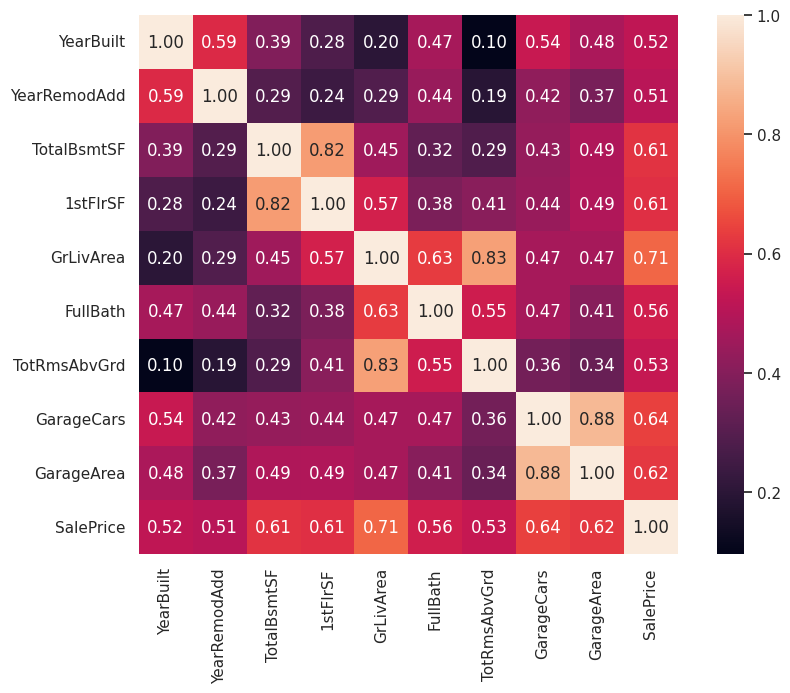
目的変数 SalePrice との相関が比較的大きな変数(0.6以上)は次の変数です。
- GrLivArea
- GarageCars
- GarageArea
- TotalBsmtSF
- 1stFlrSF
以降では、次の2つのモデルを構築して、学習、予測、評価を行ってみます。
- GrLivArea のみを説明変数にした線形単回帰モデル
- GrLivArea、GarageCars、GarageArea、TotalBsmtSF、1stFlrSF を説明変数にした線形重回帰モデル
線形単回帰による分析
ここでは次の線形単回帰モデルを考えます。
- 説明変数:GrLivArea
- 目的変数:SalePrice
前処理
データを機械学習で扱いやすいような形に前もって処理しておくことを、データの前処理といいます。 ここでは前処理として、標準化と呼ばれる手法を適用します。 標準化後のデータは平均が0、標準偏差が1となるように変換されます。
from sklearn.preprocessing import StandardScaler
high_correlated_columns = ['GrLivArea']
target_column = ['SalePrice']
X = df[high_correlated_columns]
y = df[target_column]
# 説明変数を標準化
ss_x = StandardScaler()
ss_x.fit(X)
X_scaled = ss_x.transform(X)
# 目的変数を標準化
ss_y = StandardScaler()
ss_y.fit(y)
y_scaled = ss_y.transform(y)標準化できていることを確認するために、統計量を計算してみます。
pd.DataFrame(np.hstack([X_scaled, y_scaled]),
columns=high_correlated_columns+target_column).describe()| GrLivArea | SalePrice | |
| count | 1.460000e+03 | 1.460000e+03 |
| mean | -1.277517e-16 | 1.362685e-16 |
| std | 1.000343e+00 | 1.000343e+00 |
| min | 2.249120e+00 | -1.838704e+00 |
| 25% | -7.347485e-01 | -6.415162e-01 |
| 50% | -9.797004e-02 | -2.256643e-01 |
| 75% | 4.974036e-01 | 4.165294e-01 |
| max | 7.855574e+00 | 7.228819e+00 |
平均(mean)がほぼ0、標準偏差(std)がほぼ1になっており、正しく標準化できていることが分かります。
データセットを学習用と評価用に7:3の比率で分割します。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, test_size=0.3, random_state=0)以降では、学習用データを使って学習を行い、評価用データを使ってモデルの最終的な評価を行います。
学習
sklearn.linear_model.SGDRegressor で確率的勾配降下法を使用した線形回帰モデルを構築することができます。
SGDRegressor のメソッド fit で学習することができます。 学習用データを用いて、次の条件で学習を実施します。
- エポック数:1000
- 学習係数:0.001
- 許容誤差:1.0×10−5
from sklearn.linear_model import SGDRegressor
# モデルを定義
model = SGDRegressor(max_iter=1000, eta0=0.001, learning_rate='constant', tol=1e-5, random_state=0)
# 教師データを与えて学習を実施
model.fit(X_train, y_train.ravel())学習済みの重み係数は SGDRegressor.intercept_ や SGDRegressor.coef_ から取得できます。
w0 = model.intercept_
w1 = model.coef_w0, w1(array([-0.01555789]), array([0.72015289]))補足:学習曲線
一般的に、学習に使用するサンプル数が少ない場合は、モデルがそれらのサンプルに完全に適合することが可能なため、次のような傾向があります。
- 学習用データに対する予測精度:良い
- 評価用データに対する予測精度:悪い
一方、学習に使用するサンプル数が増えてくると、すべてのサンプルに完全に適合することは難しくなりますが、汎用的なモデルに近付いていくため、次のような傾向があります。
- 学習用データに対する予測精度:悪くなる
- 評価用データに対する予測精度:良くなる
学習曲線がこのような振る舞いと異なる場合には何か問題がある可能性があるため、何らかの見直しが必要となります。
なお、学習曲線は過学習の検出にも使用されます。 過学習とはモデルが学習用データに過剰に適合した状態であり、学習用データに対する予測精度は高いのに、評価用データに対する予測精度は低い状態です。 汎化性能が低くなってしまう(未知データに対するモデルの予測精度が低くなってしまう)ため、過学習は避けなければなりません。
SGDRegressor からは学習曲線を描画するための情報を直接得られないため、ここでは、sklearn.model_selection.LearningCurveDisplay を使用して、学習曲線をプロットしてみます。 LearningCurveDisplay の引数に渡すデータは内部で学習用と検証用に分割されて、学習用データでの予測結果の評価と検証用データでの予測結果の評価が行われます。
from sklearn.model_selection import LearningCurveDisplay, ShuffleSplit
estimator = SGDRegressor(max_iter=1000, eta0=0.001, learning_rate='constant', tol=1e-5, random_state=0)
common_params = {
'X': X_train,
'y': y_train,
'train_sizes': np.linspace(0.1, 1.0, 10),
'cv': ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
'score_type': 'both',
'n_jobs': 4,
'line_kw': {'marker': 'o'},
'std_display_style': 'fill_between',
'scoring': 'neg_mean_squared_error',
'negate_score': True,
'score_name': 'Mean Squared Error',
}
LearningCurveDisplay.from_estimator(estimator, **common_params)
plt.legend(['Training score', 'Validation score'])
plt.show()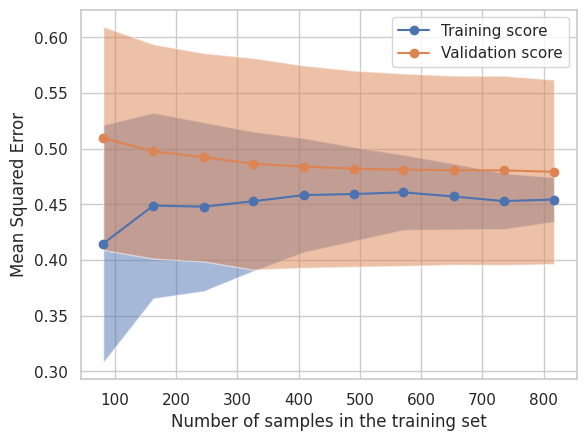
なお、上記グラフの横軸は学習に使用したサンプル数を表し、縦軸は平均二乗誤差を表しています。
予測
予測を行うにはメソッド SGDRegressor.predict を使用します。
まず、学習用データに対する予測を実行してみます。y_pred_train = model.predict(X_train)次に、評価用データに対する予測を実行してみます。
y_pred_test = model.predict(X_test)学習済みの重み係数を用いて回帰直線をプロットしてみると、次のようになります。
# 学習済みモデルでの予測をプロットするためのデータを作成
x = np.arange(np.min(X_scaled), np.max(X_scaled), 0.1)
y_pred = w0 + w1.ravel() * x
sns.scatterplot(x=X_train.ravel(), y=y_train.ravel(), marker='o', label='train')
sns.scatterplot(x=X_test.ravel(), y=y_test.ravel(), marker='s', label='test')
sns.lineplot(x=x, y=y_pred, color='green', label='trained model')
plt.xlabel('GrLivArea (scaled)')
plt.ylabel('SalePrice (scaled)')
plt.legend()
plt.show()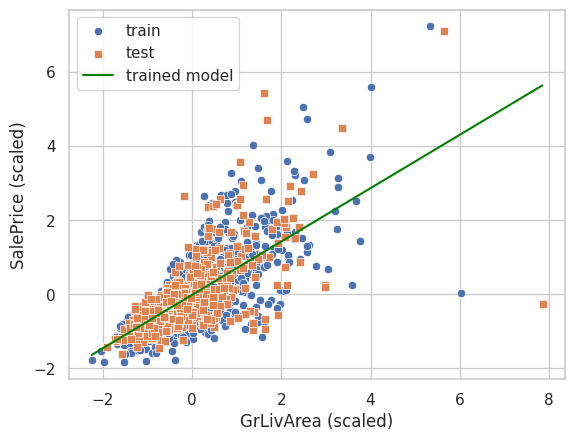
なお、ここで求めた予測値は標準化した説明変数に対する予測値であることに注意が必要です。 今回の場合、住宅価格を予測していますが、標準化された説明変数での予測結果は、例えば0.1のような数値になっており、そのままでは価格として解釈しにくいです。 そこで、予測値に対して標準化の逆変換を行って、価格として解釈可能な元のスケールに戻してから、予測値を活用します。
評価
予測結果と正解値を用いて、平均二乗誤差を計算してみます。 平均二乗誤差は sklearn.metrics.mean_squared_error によって計算できます。
from sklearn.metrics import mean_squared_error
# 学習データに対する予測の平均二乗誤差
mse_train = mean_squared_error(y_train, y_pred_train)
# 評価データに対する予測の平均二乗誤差
mse_test = mean_squared_error(y_test, y_pred_test)
print(f'train: MSE={mse_train:.3f}')
print(f'test : MSE={mse_test:.3f}')train: MSE=0.458
test : MSE=0.591また、残差プロットを描画してみます。
y_residuals_train = y_train.ravel() - y_pred_train.ravel()
y_residuals_test = y_test.ravel() - y_pred_test.ravel()
sns.scatterplot(x=y_pred_train.ravel(), y=y_residuals_train, marker='o', label='train')
sns.scatterplot(x=y_pred_test.ravel(), y=y_residuals_test, marker='s', label='test')
plt.xlabel('predicted SalePrice (scaled)')
plt.ylabel('residual')
plt.legend()
plt.show()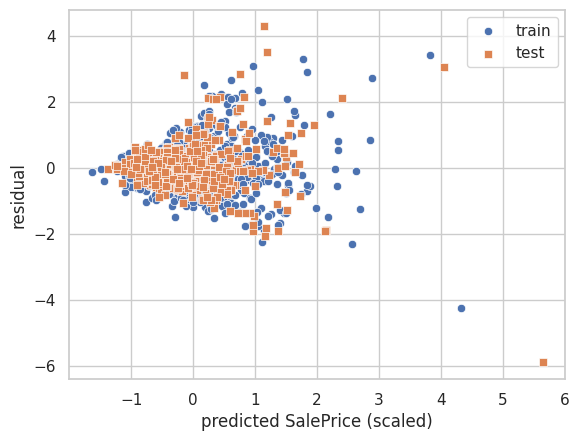
線形重回帰による分析
ここでは次の線形重回帰モデルを考えます。
- 説明変数:GrLivArea
- 目的変数:SalePrice, GarageCars, GarageArea, TotalBsmtSF, 1stFlrSF
前処理
前処理として、データを標準化します。
from sklearn.preprocessing import StandardScaler
high_correlated_columns = ['GrLivArea', 'GarageCars', 'GarageArea', 'TotalBsmtSF', '1stFlrSF']
target_column = ['SalePrice']
X = df[high_correlated_columns]
y = df[target_column]
ss_x = StandardScaler()
ss_x.fit(X)
X_scaled = ss_x.transform(X)
ss_y = StandardScaler()
ss_y.fit(y)
y_scaled = ss_y.transform(y)標準化できていることを確認するために、統計量を計算してみます。
pd.DataFrame(np.hstack([X_scaled, y_scaled]),
columns=high_correlated_columns+target_column).describe()| GrLivArea | GarageCars | GarageArea | TotalBsmtSF | 1stFlrSF | SalePrice | |
| count | 1.460000e+03 | 1.460000e+03 | 1.460000e+03 | 1.460000e+03 | 1.460000e+03 | 1.460000e+03 |
| mean | -1.277517e-16 | 1.216683e-16 | -1.216683e-17 | 2.457699e-16 | 6.509253e-17 | 1.362685e-16 |
| std | 1.000343e+00 | 1.000343e+00 | 1.000343e+00 | 1.000343e+00 | 1.000343e+00 | 1.000343e+00 |
| min | -2.249120e+00 | -2.365440e+00 | -2.212963e+00 | -2.411167e+00 | -2.144172e+00 | -1.838704e+00 |
| 25% | -7.347485e-01 | -1.026858e+00 | -6.479160e-01 | -5.966855e-01 | -7.261556e-01 | -6.415162e-01 |
| 50% | -9.797004e-02 | 3.117246e-01 | 3.284429e-02 | -1.503334e-01 | -1.956933e-01 | -2.256643e-01 |
| 75% | 4.974036e-01 | 3.117246e-01 | 4.820057e-01 | 5.491227e-01 | 5.915905e-01 | 4.165294e-01 |
| max | 7.855574e+00 | 2.988889e+00 | 4.421526e+00 | 1.152095e+01 | 9.132681e+00 | 7.228819e+00 |
平均(mean)がほぼ0、標準偏差(std)がほぼ1になっており、正しく標準化できていることが分かります。
データセットを学習用と評価用に7:3の比率で分割します。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled, test_size=0.3, random_state=0)学習
学習用データを用いて、次の条件で学習を実施します。
- エポック数:1000
- 学習係数:0.001
- 許容誤差:1.0×10−5
from sklearn.linear_model import SGDRegressor
model = SGDRegressor(max_iter=1000, eta0=0.001, learning_rate='constant', tol=1e-5, random_state=0)
model.fit(X_train, y_train.ravel())学習済みの重み係数 wi(i=0,1,…,5) の値は、SGDRegressor の属性 intercept_ と coef_ で取得できます。
w0 = model.intercept_
ws = model.coef_w0, ws(array([-0.01152539]),
array([ 0.45168704, 0.17921672, 0.11468922, 0.32918174, -0.03849689]))学習曲線をプロットしてみます。
from sklearn.model_selection import LearningCurveDisplay, ShuffleSplit
estimator = SGDRegressor(max_iter=1000, eta0=0.001, learning_rate='constant', tol=1e-5, random_state=0)
common_params = {
'X': X_train,
'y': y_train,
'train_sizes': np.linspace(0.1, 1.0, 10),
'cv': ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
'score_type': 'both',
'n_jobs': 4,
'line_kw': {'marker': 'o'},
'std_display_style': 'fill_between',
'scoring': 'neg_mean_squared_error',
'negate_score': True,
'score_name': 'Mean Squared Error',
}
LearningCurveDisplay.from_estimator(estimator, **common_params)
plt.legend(['Training score', 'Validation score'])
plt.show()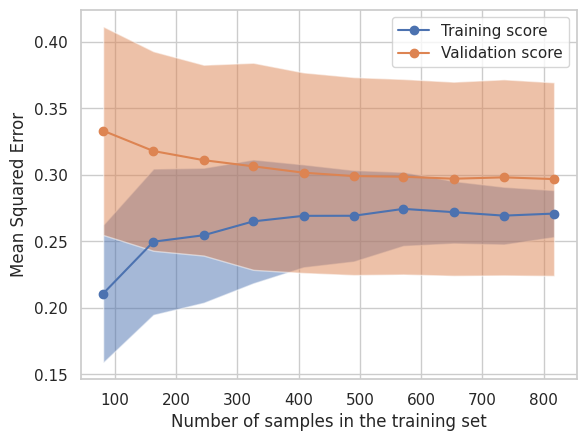
予測
学習用データに対する予測を実行します。
y_pred_train = model.predict(X_train)また、評価用データに対する予測を実行します。
y_pred_test = model.predict(X_test)なお、単回帰では回帰直線を2次元平面上にプロットできましたが、重回帰では次元数が増えるため、2次元平面では図示できません(※説明変数が2個の場合は3次元空間中に回帰平面として図示できます)。
評価
学習用データおよび評価用データに対する予測の平均二乗誤差は、それぞれ次のとおりです。
# 学習データに対する予測の平均二乗誤差
mse_train = mean_squared_error(y_train, y_pred_train)
# 評価データに対する予測の平均二乗誤差
mse_test = mean_squared_error(y_test, y_pred_test)
print(f'train: MSE={mse_train:.3f}')
print(f'test : MSE={mse_test:.3f}')train: MSE=0.275
test : MSE=0.431説明変数を増やしたことによって、学習データについても評価データについても、線形単回帰のときよりも平均二乗誤差の値が改善している(小さくなっている)ことが分かります。
また、残差プロットは次のとおりです。
y_residuals_train = y_train.ravel() - y_pred_train.ravel()
y_residuals_test = y_test.ravel() - y_pred_test.ravel()
sns.scatterplot(x=y_pred_train.ravel(), y=y_residuals_train, marker='o', label='train')
sns.scatterplot(x=y_pred_test.ravel(), y=y_residuals_test, marker='s', label='test')
plt.xlabel('predicted SalePrice (scaled)')
plt.ylabel('residual')
plt.legend()
plt.show()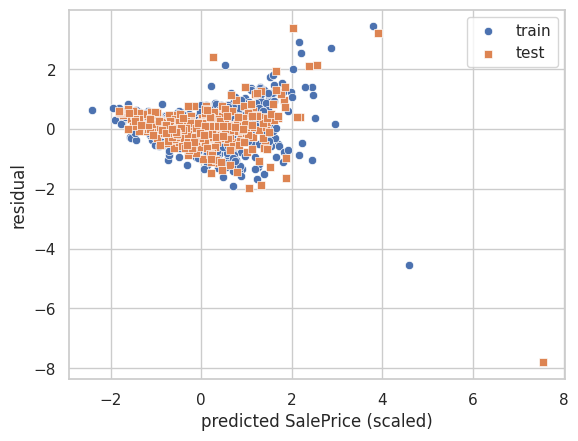
今回はこれで以上になります。
次回はアヤメの分類をテーマにして、機械学習の基本的なタスクである「分類」を取り扱います。
最後までお読みいただきありがとうございました。それでは引き続きよろしくお願いいたします。




